Question

What is the number for the expression once it is simplified? This should not have any exponents. ((64x-⁹y-¹⁵) ⅓)/ ((8²x-¹²y¹⁰)½)

Answer 1

The expression to simplify is:

`\frac{(64x^(-9)y^(-15))^{(1)/(3)}}{(8^2x^(-12)y^(10))^{(1)/(2)}}`

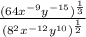
We can use the property shown below to simplify it:

`(a^m)^n=a^(mn)`

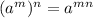
Thus, we can write:

`\begin{gathered} \frac{(64x^(-9)y^(-15))^{(1)/(3)}}{(8^2x^(-12)y^(10))^{(1)/(2)}} \\ =\frac{(64)^{(1)/(3)}(x^(-9))^{(1)/(3)}(y^(-15))^{(1)/(3)}}{(64)^{(1)/(2)}(x^(-12))^{(1)/(2)}(y^(10))^{(1)/(2)}} \end{gathered}`

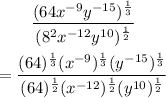
64 to 1/3rd power is 4

64 to 1/2 power is 8

Thus, further simplifying, we have:

`\begin{gathered} \frac{(64)^{(1)/(3)}(x^(-9))^{(1)/(3)}(y^(-15))^{(1)/(3)}}{(64)^{(1)/(2)}(x^(-12))^{(1)/(2)}(y^(10))^{(1)/(2)}} \\ =(4x^(-3)y^(-5))/(8x^(-6)y^5) \end{gathered}`

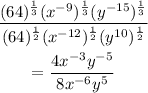
We can use the rule

`(x^a)/(x^b)=x^(a-b)`

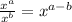
to bring up all the exponents and get the simplified form:

`\begin{gathered} =(x^(-3)y^(-5)x^6y^(-5))/(2) \\ =(x^3y^(-10))/(2) \end{gathered}`

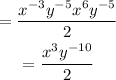
This is the final answer.

The exponent of x is 3 and the exponent of y is -10.