Question

What is the value of x? Type your answer in numerical value only.

Answer 1

Answer: " x = 7 ".
____

{Note: If one is interested, the following information provides a "step-by-step" explanation.}:

____

Method 1)

Make a ratio:
"(2x + 10) : 40 :: 3:5 " ;

Write this ratio in the form of a fraction:
→ "
`((2x+10))/(40)=(3)/(5)` ";
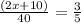Cross-factor multiply :
Note: Given: "
`(a)/(b) = (c)/(d)` " ; "
`ad = bc`" ; ["
`b\\eq 0 ; d\\eq 0`"] ;
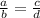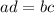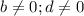→As such: "
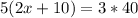`5(2x+10) = 3 * 40` " ; Solve for "x";
⇒ { 5(2x + 10} / 5 = (3 * 40)/5 ; ⇒ 2x + 10 = 120/5 ;

to get: 2x + 10 = 24 ;
→ or: "{5(2x + 10}/5 =
`(4*30)/(5)` ";

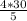⇒ On the "right-hand side" of the equation:
The "30" in the numerator cancels to "6" ; and the "5" in the denominator cancels to "1" ; {since: "30÷5 = 6" ; & since: "6÷6 = 1"} ;

and we can rewrite the equation:
⇒ 2x + 10 = 24 ; → Subtract "10" from each side of the equation:
→ 2x + 10 - 10 = 24 - 10 ; to get: " 2x = 14 " ;

⇒Now, divide each side of the equation by "2" ;

to isolate "x" on one side of the equation; & to solve for "x" :
→ 2x/2 = 14/2 ; to get: " x = 7 " .
________
Alternately, when we have: " 2x + 10 = 24 " ; we can simplify this equation by dividing each side of the equation by "2" ;
________
⇒ {2x+10}/2 = {24/2} ;
to get: → (2x/2) + (10/2) = (24/2); → to get: "x + 5 = 7" ;

⇒ Then: Subtract "5" from each side of the equation; to isolate "x" on one side of the equation; & to solve for "x" ;
⇒ x + 5 - 5 = 12 - 5 ; to get: " x = 7 " ;
________

Method 2)

Write this ratio in the form of a fraction:
→ "
`((2x+10))/(40)=(3)/(5)` " ;
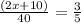Cross-factor multiply :
Note: Given: "
`(a)/(b) = (c)/(d)` " ; "
`ad = bc`" ; ["
`b\\eq 0 ; d\\eq 0`"] ;
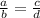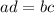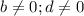As such: → "
`5(2x+10) = 3 * 40` " ;
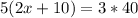⇒ Now; to solve for "x" ; → "
`5(2x+10) = 3 * 40` " ;

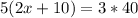⇒ Note: Re: the "left-hand side" of the equation:
________

" 5(2x + 10) " ;

Note the "distributive property of multiplication" :
⇒ a(b + c) = ab + ac ;
As such:
→ "
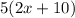`5(2x+10)` " ↔= " (5*2x) + (5*10) = (10x) + (50) = 10x + 50 ;
→ Then, take note of the "right-hand side" of the equation:

⇒ (40*3) = 120 ;
→ Now, we can rewrite the equation as: " 10x + 50 = 120 " ;
⇒To solve for "x": We can subtract "50" from each side of the equation:
⇒ 10x + 50 - 50 = 120 - 50 ; → to get: "10x = 70 " ;
→ Now, we can divide each side of the equation by "10"; to isolate "x" on one side of the equation; & to solve for "x" ;
________
10x/10 = 70/10 ; to get: "x = 7" .
________
Alternately: " 10x + 50 = 70 " ; Solve for "x" ;
→ Divide each side of the equation by "10"; to simplify the equation:
→{10x+50}/10 = 120/10 ; → (10x/10) + (50/10) = 12;
→ to get: → "x+5 = 12"; Then: Subtract "5" from each side of the equation; to isolate "x" on one side of the equation; & to solve for "x ;
→ x + 5 - 5 = 12 - 5 ; → to get: " x = 7 " ;
________

Alternately: We have: "10x + 50 = 120"; Solve for "x";
→ Factor out a "10" in the "left-hand-side" of the equation:
⇒ 10(a ± b) = 120 ; Now; Solve for "a" and for "b" :
⇒ To solve for a: →" 10a=10x "; Divide each side of the equation by "10" ; to isolate "a" on one side of the equation; & to solve for "a":
⇒ "10a/10 = 10x/10"; to get: → a = ⁺1x = ⁺x ; → "a = x";
⇒ To solve for b : " 10b = 50 "; Divide each side of the equation by "10";
to isolate "b" on one side of the equation; & to solve for "b" ;
⇒ " 10b/10 = 50/10 "; to get: "b = ⁺5";
→ So; we can rewrite the equation as: "10(x + 5) = 120"; →To solve for "x" ; ⇒ Let us divide each side of the equation by "10" ;

⇒"{10(x+5)}/10 = 120/10"; → to get: "x + 5 = 12" ;
→ Then: Subtract "5" from each side of the equation;
to isolate "x" on one side of the equation; & to solve for "x";
→ x + 5 - 5 = 12 - 5 ; → to get: " x = 7 " ;
____

Alternately: → "
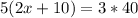`5(2x+10) = 3 * 40` " ; Solve for "x" :
→ Divide each side of the equation by "5";
→ {5(2x+10}/ 5 = (3*40)/5 ; → to get: 2x + 10 = (120)/5;
to get: "2x + 10 = 40" ; and then continue using any of the variant methods described above; to get: "x = 7" .
____
The answer would be "x = 7 cm" ; but the question asks for only a numerical value; & since both [two of the three] given measurements (in the imaged attached) are in units of "cm" ["centimeters"], we shall assume the units of measurements are all the same (in "cm"); since there is no indication to the contrary.
____
Hope this helps!
____