Question

Suppose that the functions g and h are defined as follows.g(x) = -4+3x²h(x)=2-8x(a) Find(3)(-1).(b) Find all values that are NOT in the domain ofhIf there is more than one value, separate them with commas.

Answer 1

From the given functions :

`\begin{gathered} g(x)=-4+3x^2 \\ h(x)=2-8x \end{gathered}`

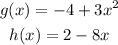
a. Find (g/h)(-1)

We need to find first the function (g/h) then substitute x = -1

`\begin{gathered} ((g)/(h))(x)=(-4+3x^2)/(2-8x) \\ ((g)/(h))(-1)=(-4+3(-1)^2)/(2-8(-1))=(-1)/(10) \end{gathered}`

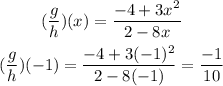
Therefore, the answer is -1/10

b. Find all values that are NOT in the domain.

Domain is the set of x values that will make the function (g/h)(x) be defined.

Note that the function will be UNDEFINED if the denominator is equal to 0.

Thus, we need to equate the denominator to 0. To get the values of x, which are NOT in the domain.

The denominator is 2 - 8x, let's equate it to 0, then solve for x :

`\begin{gathered} 2-8x=0 \\ -8x=-2 \\ x=(-2)/(-8)=(1)/(4) \end{gathered}`

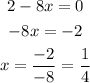
Therefore, the values that are NOT in the domain is 1/4