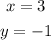Question

Can you solve theis by the system of linear equations by elimination

Answer 1

To solve the system of equation using elimination, notice that the coefficient of the variable y appears with -3 in one equation and with 3 in the other. Since 3 and -3 are additive inverse numbers, then they will cancel out when added.

Then, add both equations: left hand side plus left hand side equals right hand side plus right hand side:

`\begin{gathered} 2x-3y=9 \\ 5x+3y=12 \\ \Rightarrow2x-3y+5x+3y=9+12 \\ \Rightarrow2x+5x-3y+3y=21 \\ \Rightarrow7x=21 \\ \Rightarrow x=(21)/(7) \\ \Rightarrow x=3 \end{gathered}`

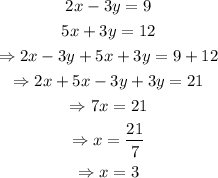
Substitute back x=3 in one of the equations and solve for y:

`\begin{gathered} 5x+3y=12 \\ \Rightarrow5(3)+3y=12 \\ \Rightarrow15+3y=12 \\ \Rightarrow3y=12-15 \\ \Rightarrow3y=-3 \\ \Rightarrow y=-(3)/(3) \\ \Rightarrow y=-1 \end{gathered}`

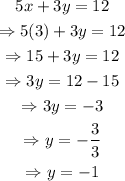
Therefore, the solution to this system, is:

`\begin{gathered} x=3 \\ y=-1 \end{gathered}`