Question

the area of mark’s rectangular garden is (3x^2+4x-4) square feet. The width is (x+2) ft.a.what is the length of the garden?b.Find the perimeter of the garden in terms of x.c.The cost of fertilizer is $0.25 per square foot. what is the cost of fertilizer when x is 6

Answer 1

We know that the area is determined by the equation

`3x^2+4x-4`

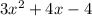
And the width is

`(x+2)`

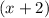
First of all, remember that the area of a rectangle is

`A=w\cdot l`

Where the length would be

`l=(A)/(w)`

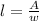
Before we use this length expression, first we need to find the solutions for the given quadratic equation. Using a calculator, the solutions are 2/3 and -2. Only the number 2/3 makes sense to the problem since length can't be negative.

Expressing these solutions as factors would be

`3x^2+4x-4=(3x-2)(x+2)`

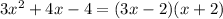
Now, we replace all factors to find the length

`l=(\left(3x-2\right)\left(x+2\right))/(x+2)=3x-2`

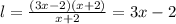
Therefore, the length is (3x-2) feet.

On the other hand, the perimeter is the sum of all sides, also it can be expressed as

`P=2(l+w)`

Using the length and width expressions

`P=2(3x-2+x+2)=2(4x)=8x`

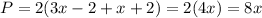
Therefore, the perimeter is (8x) feet.

When x is 6, the area would be

`3x^2+4x-4=3(6)^2+4(6)-4=3(36)+24-4=108+20=128`

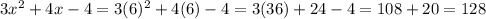
The area is 128 square feet. Now, if the cost of the fertilizer is $0.25, the total cost for the area would be

`C=128(0.25)=32`

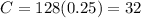
Therefore, the total cost is $32 per square foot.