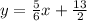Given:
The point given is
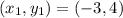
and the slope is
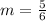
Required:
Point-slope form of a line passing through given point.
Answer:
Here, we use the point-slope form of a line passing through the point
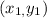
and having slope
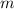
is given by,
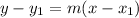
Thus, by substituting the values, the point-slope form of a line passing through the given point is,
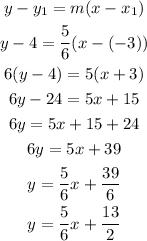
Final Answer:
The point-slope form of a line passing through the given point is,