Question

A company sells one of its products for $32 each. The monthly fixed costs are $3800. The marginal cost of the produce is $12. Let q = quantity and C(q) = cost.a) Express the total monthly costs, C, as a function of q, the quantity produced each monthC(q) = b) Express the total monthly revenue, R, as a function of the quantity, q, sold each monch.R(q) =c) Find the quantity, q, produced and sold each month at which this company will break even. Round your answer to a whole number.

Answer 1

a)

The monthly cost is composed by the fixed cost of $3800 plus the cost of production, which is $12 per unit.

If the company produced q products, the cost C(q) is:

`C(q)=3800+12q`

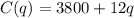
b)

The revenue is given by the products sold, which are worth $32 per unit.

Since the number of products is q, the revenue is:

`R(q)=32q`

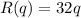
c)

To find the quantity q so the company will break even (that is, profit = 0), let's equate the revenue and the cost and then calculate the value of q:

`\begin{gathered} \text{profit}=\text{revenue}-\text{cost} \\ 0=\text{revenue}-\text{cost} \\ \text{revenue}=\text{cost} \\ R(q)=C(q) \\ 32q=3800+12q \\ 32q-12q=3800 \\ 20q=3800 \\ q=190 \end{gathered}`

Therefore the quantity q is equal to 190 units.