Question

A baseball is hit, following a path represented by x = 130t and y = 3.2 + 42t − 16t 2 for 0 ≤ t ≤ 3.

Answer 1

Part A)

Evaluate x(t) and y(t) at t=0.2, 1.2 and 2.4 to find the ordered pairs.

`\begin{gathered} x=130t \\ y=3.2+42t-16t^2 \end{gathered}`

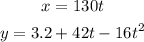
t=0.2

`\begin{gathered} x=130*0.2=26 \\ y=3.2+42*0.2-16*0.2^2=10.96 \end{gathered}`

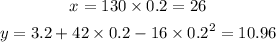
Then, the ordered pair for t=0.2 is (26,10.96).

t=1.2

`\begin{gathered} x=130*1.2=156 \\ y=3.2+42*1.2-16*1.2^2=30.56 \end{gathered}`

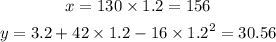
Then, the ordered pair for t=0.2 is (156,30.56).

t=2.4

`\begin{gathered} x=130*2.4=312 \\ y=3.2+42*2.4-16*2.4^2=11.84 \end{gathered}`

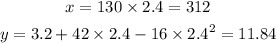
Then, the ordered pair for t=2.4 is (312,11.84).

Part B)

Find a rectangular equation (y as a function of x) to find the height of the ball when it reaches a horizontal distance of 320ft. To do so, isolate t from the equation for x:

`\begin{gathered} x=130t \\ \Rightarrow t=(x)/(130) \end{gathered}`

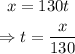
Replace t=x/130 into the equation for y:

`\begin{gathered} y=3.2+42t-16t^2 \\ \Rightarrow y=3.2+42((x)/(130))-16((x)/(130))^2 \\ \Rightarrow y=3.2+(42)/(130)x-16*(x^2)/(16,900) \\ \Rightarrow y=3.2+(42)/(130)x-(16)/(16,900)x^2 \\ \Rightarrow y=3.2+(42)/(130)x-(4)/(4,225)x^2 \end{gathered}`

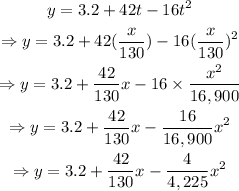
Replace x=320 to find the height of the ball:

`y=3.2+(42)/(130)(320)-(4)/(4225)(320)^2=9.6378...`

Since the height of the ball is less than the height of the fence when it reaches a horizontal distance of 320ft, then the baseball doesn't travel over the fence.

Part C)

A rectangular equation to represent the plane curved was already found in Part B:

`y=3.2+(42)/(130)x-(4)/(4225)x^2`