1 Answer

Arun Chettoor · Answer 1 · 2023-01-24T15:27:08+0000

We have two unknowns (x and y) and 2 equations.

We will clear one unknown in the first equation and then replace it in the second.

Then, we can solve for the other variable and solve backwards.

The first equation is:

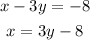
$\begin{gathered} x-3y=-8 \\ x=3y-8 \end{gathered}$

We replace the value of x in the second equation:

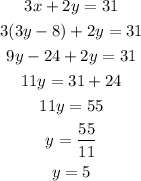
$\begin{gathered} 3x+2y=31 \\ 3(3y-8)+2y=31 \\ 9y-24+2y=31 \\ 11y=31+24 \\ 11y=55 \\ y=(55)/(11) \\ y=5 \end{gathered}$

Then, with y=5, we can calculate the value of x:

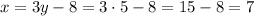
$x=3y-8=3\cdot5-8=15-8=7$

The solution (x,y) is (7,5). The answer is Option D.

Please log in or register to add a comment.