Question

What is the vertex form of the quadratic function that has a vertex at (2, 1) and goes through the point (3, 2)? O A. y = (x - 2)2 + 1 B. y = 3(x - 2)2 + 1 OC. y = –2(x + 2)2 - 1 OD. y=-3(x - 2)2 + 1

Answer 1

Choice D.

Step-by-step explanation:

The vertex form of a parabola is given by

`y=a(x-h)^2+k`

where (h, k) is the vertex.

Now, in our case we have the vertex at (2, 1); therefore, the above gives

`y=a(x-2)^2+1`

Now we just need to find the value of a.

We know that the parabola passes through the point (3, -2), meaning the equation must satisfy x= 3 when y = -2.

Putting in x = 3 and y = -2 in the above equation gives

`-2=a(3-2)^2+1`

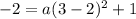
which simplifies to give

`-2=a+1`

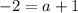
subtracting 1 from both sides gives

`a=-3`

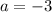
Hence, the equation of the quadratic function is

`y=-3(x-2)^2+1`

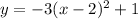
which is choice D.