Question

I would like to get help on this question please! And how to solve it

Answer 1

We are given the following product

`(1\text{ -x\rparen}\cdot(x+3)\cdot(7x+3)^2`

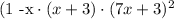
we want to find the degree, leading coefficient and constant coefficient of this product. To do so, we should find first this quantities from each of the polynomials.

Recall that the degree of the polynomial is the highest power of the variable (in this case x). Recall that the leading coefficient is the coefficient that is multiplying the power of x with the highest degree. Finally, recall that the constant coefficient of the polynomial is the coefficient that has no variable.

So we have

`(1\text{ -x\rparen}`

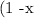
in this case, the highest power of x is 1. So the degree of this polynomial is 1. In this case, the coefficient that multiplies the highest power of x is -1. So the leading coefficient is -1. Finally, the constant coefficient is 1.

For the other polynomial we have

`(x+3)`

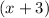
in this case the degree is 1, the leading coefficient is 1 and and the constant coefficient is 3.

Finally, for the other polynomial we have

`(7x+3)^2=49x^2+42x+9`

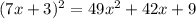
so for this polynomial, the degree is 2, the leading coefficient is 49 and the constant coefficient is 9.

Now, we simply use this information to calculate it for the whole product.

The degree of the polynomial is the sum of all degrees. So the degree of the polynomial is 1+1+2=4.

The leading coefficient is the product of the leading coefficients. So the leading coefficient is -1*1*49=-49.

The constant coefficient is the product of the constant coefficients. So the constant coefficient is 1*3*9=27.