Question

a half life of a certain radioactive material is 10 hours and initial amount of the material has a mass of 75 Kg. find how long it will take until there is 15 kg of the radioactive material remaining

Answer 1

a half life of a certain radioactive material is 10 hours and initial amount of the material has a mass of 75 Kg. find how long it will take until there is 15 kg of the radioactive material remaining ​

we know that

the equation that represent this situation is an exponential function of the form

`y=a((1)/(2))^t`

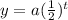
where

a is the initial value

t is the time in hours

t=time/half life

y is the mass

In this problem we have

a=75 kg

t=t/10

so

substitute

`y=75((1)/(2))^{((t)/(10)))}`

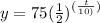
For y=15 kg

substitute in the equation above

`\begin{gathered} 15=75((1)/(2))^{((t)/(10)))} \\ (15)/(75)=(0.5)^{((t)/(10))} \\ \text{apply log both sides} \\ \log ((15)/(75))=(t)/(10)\cdot\log (0.5) \\ t=10\cdot\log ((15)/(75))\colon\log (0.5) \\ t=23.2\text{ hours} \end{gathered}`

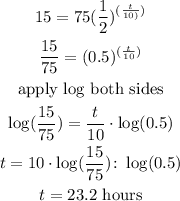
therefore

the answer is 23.2 hours