Question

Exercises 12.3 Complete the following: 1. Complete the squares for each quadratic, list the center labeling its translated center: (a) x2 + 2x + y2 – 4y = 4 (c) 2x2 + 2y2 + 3x - 5y = 2 (e) x2 + y2 + 3x = 4 (g) x2 + y2 + 4x = 0 (i) x2 + y2 + 2mx 2ny = 0 (b) (d -Letter g

Answer 1

(x + 2)² + y² = 4

Step-by-step explanation:

If we have an equation with the form:

x² + bx = c

We can complete the square by adding (b/2)² to both sides.

In this case, we have:

x² + y² + 4x = 0

So, we can organize the terms as:

(x² + 4x) + y² = 0

Therefore, to complete the square of (x² + 4x) we need to add:

`((b)/(2))^2=((4)/(2))^2=2^2=4`

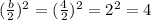
Then:

(x² + 4x + 4) + y² = 0 + 4

(x + 2)² + y² = 4

On the other hand, the equation of a circumference is:

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) is the center and r is the radius.

So, we can rewrite the equation as:

(x + 2)² + y² = 4

(x -(-2)² + (y - 0)² = 2²

Therefore, the center is the point (-2, 0) and the radius is 2. So, the graph of the circle is: