Step-by-step explanation:
First, we need to graph the equality y = x² + 2x - 3
So, to graph the parabola, we need to identify the vertex and 2 points in the parabola.
The vertex can be calculated as:

Where b is the number beside the x and a is the number beside the x². Then the value of y is equal to:
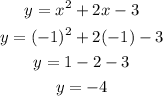
So, the vertex (- 1, - 4)
Then, to find 2 points in the parabola we can replace x by 0 and x by -2 as:
For x = 0
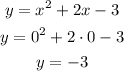
For x = -2
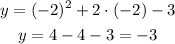
Therefore, we have the vertex (-1, -4) and the points (0, -3) and (-2, -3)
Then, the inequality is y less or equal than the parabola so, the zone for the inequality is:
So, the graph of the inequality is the region below the graph of the parabola.