Question

A man on a road trip drives a car at different constant speeds over several legs of the trip. He drives for 60.0 min at 60.0 km/h, 10.0 min at 80.0 km/h, and 50.0 min at 60.0 km/h and spends 55.0 min eating lunch and buying gas.(a)What is the total distance traveled over the entire trip (in km)? km(b)What is the average speed for the entire trip (in km/h)? km/h

Answer 1

a) 123.33 km

Step-by-step explanation:

Part (a)

The distance traveled on each part of the trip can be calculated as the speed times the time. So, for each part of the trip, we get:

60.0 min at 60.0 km/h

First, we need to convert 60 min to hour. Since 60 min = 1 hour, we get:

distance = (60 km/h)(1 h)

distance = 60 km

10.0 min at 80.0 km/h

First convert 10 min to hour s

`10.0\text{ min}*\frac{1\text{ hour}}{60.0\text{ min}}=(1)/(6)\text{ hour}`

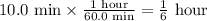
Then, the distance is

distance = (80.0 km/h)(1/6 hour)

distance = 13.33 km

50.0 min at 60.0 km/h

First convert 50 min to hours

`50\text{ min}*\frac{1\text{ hour}}{60\text{ min}}=(5)/(6)\text{ hour}`

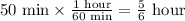
Then,

distance = (60 km/h)(5/6 hour)

distance = 50 km

Therefore, the total distance traveled over the entire trip is

Total distance = 60 km + 13.33 km + 50 km

Total distance = 123.33 km

Part (b)

Now, to calculate the average speed we will use the following:

Avg speed = Total distance / time

The total time is equal to

Time = 60 min + 10 min + 50 min + 55 min

Time = 175 min

Then, convert 175 min to hours as

`175\text{ min}*\frac{1\text{ hour}}{60\text{ min}}=2.916\text{ hours}`

Therefore, the average speed is

Avg speed = 123.33 km / 2.916 hours

Avg speed = 42.29 km/h