The initial volume is 40 liters.
The volume lost on first day is,
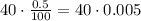
The volume left after first day leak is,
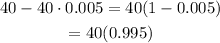
The volume leak on second day is,
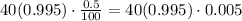
The volume left after second day leak is,
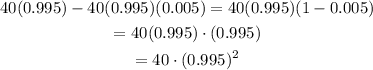
In same manner if volume decreases for seven days, then volume of gas is,
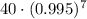
Answer: Option D