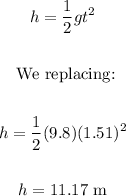ANSWER:
a) 1.51 seconds
b) 11.17 meters
Explanation:
Given:
Mass (m) = 0.3 kg
Length (l) = 25 cm = 0.25 m
Width (w) = 11 cm = 0.11 m
Terminal velocity (vt) = 14.77 m/s
Density of the air (d) = 1.225 kg/m³
Drag coefficient = 0.8
a)
We can determine the time using the following formula since we know the terminal velocity:

b)
Now, knowing the time, determine the height: