Question

(07.02 MC)Jason has two bags with 6 tiles each. The tiles in each bag are shown below:Make 6 squares. The squares are numbered sequentially from 1 to 6.Without looking, Jason draws a tile from the first bag and then a tile from the second bag. What is the probability of Jason drawing an even tile from the first bag and an even tile from the second bag? (1 point6 over 129 over 126 over 369 over 36

Answer 1

We need to find the probability of Jason drawing an even tile from the first bag and an even tile from the second bag.

Since the events of drawing a tile of each bag are independent, the final probability is the product of the two probabilities below:

• P1 ,= drawing an even tile from the first bag;

,

• P2 ,= drawing an even tile from the second bag.

Notice that the tiles are numbered from 1 to 6. Thus, three of them are even:

`2,4,6`

Therefore, the probability of drawing an even tile from the first bag is 3 out of 6:

`P_1=(3)/(6)`

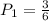
Since the second bag also has 6 tiles numbered from 1 to 6, the probability P2 is also 3 out of 6:

`P_2=(3)/(6)`

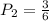
Therefore, the final probability is:

`P_1\cdot P_2=(3)/(6)\cdot(3)/(6)=(3\cdot3)/(6\cdot6)=(9)/(36)`

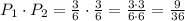
Answer

`(9)/(36)`