Given:
a.) A company will need 1.8 million 5 years from now to replace some equipment.
b.) The account pays 5.25 percent interest, compounded annually.
We will be applying the Compounded Interest Formula:
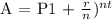
Where,
A=final amount
P=initial principal balance/money to initially deposit
r=interest rate (decimal)
n=number of times interest applied per time period
t=number of time periods elapsed (in years)
In this scenario, we are asked what is the amount of principal balance/initial deposit to make to get 1.8 million in 5 years.
Annually = n = 1
We get,
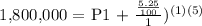

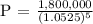
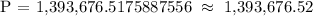
Therefore, the answer is 1,393,676.52