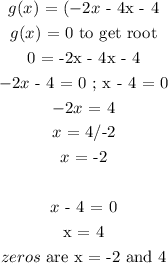Question

If anything is written unclearly, just say so and I will type it out. Thank you!

Answer 1

Answer:
`\begin{gathered} a)\text{ down \lparen see graph below\rparen} \\ b)\text{ narrow} \\ c)\text{ g\lparen x\rparen = \lparen-2x - 4\rparen\lparen x -4\rparen} \\ d)\text{ g\lparen x\rparen= -2\lparen x - 1\rparen}^2\text{ + 18} \\ e)\text{ \lparen h, k\rparen = \lparen1, 18\rparen} \\ f)\text{ x = 1} \\ h)\text{ x = -2 and 4} \end{gathered}`

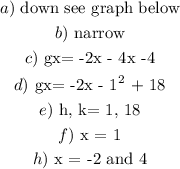
Step-by-step explanation:

Given:

`g(x)\text{ = -2x}^2\text{+4x+16}`

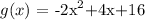
To find:

the answers to the multiple questions applicable to the function

a) The sign of the leading coefficient (coefficient of highest power) is negative, As a result, the graph will open down

b) The higher the quadratic leading coefficient, the narrower the graph

A value of like 0.5 gives a wider graph, so 2 will be seen as narrow

It is narrow

c) To get the factored form, we will factorised the given expression

`\begin{gathered} g(x)\text{ = -2x}^2\text{ + 4x + 16} \\ a\text{ = -2, b = 4, c = 16} \\ We\text{ need to find }factors\text{ of ac whose sum gives b} \\ ac\text{ = -2\lparen16\rparen= -32} \\ factors\text{ of -32 whose sum gives 4 = 8 and -4} \\ \\ g(x)\text{ = -2x}^2\text{ + 8x - 4x + 16} \end{gathered}`
`\begin{gathered} g(x)\text{ = -2x\lparen x - 4\rparen - 4\lparen x - 4\rparen} \\ g(x)\text{ = \lparen-2x - 4\rparen\lparen x - 4\rparen \lparen factored form\rparen} \end{gathered}`

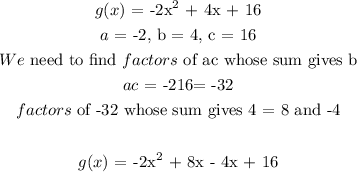
d) the vertex form of a quadratic equation is given as:

`\begin{gathered} y\text{ = a\lparen x - h\rparen}^2\text{ + k} \\ where\text{ \lparen h, k\rparen = vertex} \end{gathered}`
`\begin{gathered} We\text{ need to get h and k to complete the vertex form} \\ h\text{ = }(-b)/(2a) \\ k\text{ = g\lparen}(-b)/(2a)) \\ \\ a\text{ = -2, b = 4, c = 16} \\ h\text{ = }(-4)/(2(-2)) \\ h\text{ = }(-4)/(-4)\text{ = 1} \\ \\ k\text{ = g\lparen}(-b)/(2a))\text{ = g\lparen value of h\rparen} \\ k\text{ = g\lparen1\rparen} \\ g(1)\text{ = -2\lparen1\rparen}^2\text{ + 4\lparen1\rparen + 16} \\ g(1)\text{ = -2 + 4 + 16 = 18} \\ k\text{ = 18} \end{gathered}`
`\begin{gathered} h\text{ = 1, k = 18} \\ substitute\text{ in to the vertex form formula:} \\ y\text{ = a\lparen x - 1\rparen}^2\text{ + 18} \\ \\ leading\text{ coefficient = -2} \\ a\text{ = leading coefficient = -2} \\ y\text{ = -2\lparen x - 1\rparen}^2+\text{ 18} \end{gathered}`

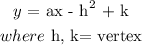
Vertex: (h, k)

`Vertex\text{ = \lparen1, 18\rparen}`

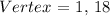
Axis of symmetry: The value of x which gives a mirror image when the parabola is split into two

The axis of symmetry is the value of h in the vertex. h = 1

Since it is an x coordinate, the axis of symmetry is x = 1

Roots are the values of x which makes the function equal to zero

We will use the factored form to get x

`\begin{gathered} g(x)\text{ = }(-2x\text{ - 4\rparen\lparen x - 4\rparen} \\ g(x)\text{ = 0 to get root} \\ 0\text{ = \lparen-2x - 4\rparen\lparen x - 4\rparen} \\ -2x\text{ - 4 = 0 ; x - 4 = 0} \\ -2x\text{ = 4} \\ x\text{ = 4/-2} \\ x\text{ = -2} \\ \\ x\text{ - 4 = 0} \\ \text{x = 4} \\ zeros\text{ are x = -2 and 4} \end{gathered}`