Given,
A jet travels 6320 miles in 8 hours.
Flying with the wind, the same jet travels 5950 miles in 5 hours.
To find: The rate of the jet in still air, and the rate of the wind.
Solution:
The jet's velocity against the wind is
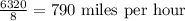
The jet's velocity with wind is
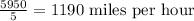
Let the velocity of the jet in still air be x miles per hour and velocity of wind be y miles per hour.
As such its velocity against wind is x-y and with wind is x+y and therefore
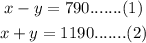
Solve both equations (1) and (2)
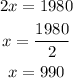
And
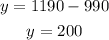
Hence, the velocity of the jet in still air is 990 miles per hour and the velocity of wind is 200 miles per hour.