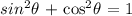Question

Use pythagorean trigonometric identities to evaluate and simplify the following expression;

Answer 1

`sin^2\theta\text{ + cos}^2\theta\text{ = 1}`

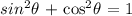
Step-by-step explanation:

Here, we want to use trigonometric identities to solve the given question

To answer this, let us have a right triangle with the sides labeled as follows:

From what we have here, a represents the hypotenuse of the right triangle which is the longest side. b faces the angle given which means it is the opposite side. c is the adjacent side

Mathematically, the sine of an angle is the ratio of the length of the opposite side to that of the hypotenuse

We have that as:

`sin\text{ }\theta\text{ = }(b)/(a)`

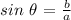
the cosine is the ratio of the length of the adjacent side to that of the hypotenuse

We have that as:

`cos\text{ }\theta\text{ = }(c)/(a)`

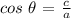
Lastly, from Pythagoras' theorem, we have it that the square of the length of the hypotenuse equals the sum of the squares of the length of the opposite and the adjacent sides

Mathematically, we have that as:

`a^2\text{ = b}^2+c^2`

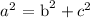
Now, let us square the sine and cosine values:

`\begin{gathered} sin^2\theta\text{ + cos}^2\theta\text{ = \lparen}(b)/(a))\placeholder{⬚}^2+((c)/(a))\placeholder{⬚}^2 \\ \\ =\text{ }(b^2+c^2)/(a^2) \end{gathered}`

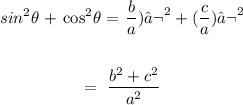
From above:

`\begin{gathered} Recall\text{ : b}^2+c^2\text{ = a}^2 \\ Thus: \\ (b^2+c^2)/(a^2)\text{ = }(a^2)/(a^2)\text{ =1} \end{gathered}`

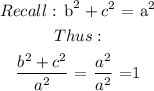
Thus, we can conclude that:

`sin^2\theta\text{ + cos}^2\theta\text{ = 1}`