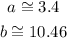We have the following triangle:
First, we start from the fact that we have an internal angle of 72 degrees and a right angle i.e. a 90-degree angle.
Second, having two internal angles, we solve and find the last internal angle.

Third, we find "a" and "b" with the law of sines, the equation of this law is:
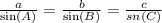
Where we have these values:
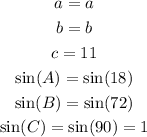
Now we solve "a"
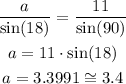
Now we solve "b"
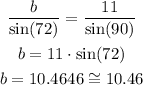
In conclusion, the answers are approximate: