Question

In an experiment, the probability that event B occurs is, and the probability that event A occurs given that event B occurs is 5 6 What is the probability that events A and B both occur? Simplify any fractions.

Answer 1

We are given the following information:

The probability that event B occurs is:

`P(B)=(3)/(5)`

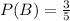
And the probability that event A occurs given that event B occurs is:

`P(A|B)=(5)/(6)`

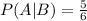
And we need to find the probability that both A and B occur.

To solve this problem, we have to use the conditional probability formula:

`P(A|B)=(P(A\cap B))/(P(B))`

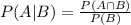
Where

P(A|B) is the probability of A given that B occurred.

P(B) is the probability of B.

And P(A∩B) is the probability of A and B occuring.

Thus, we solve for P(A∩B) in the previous equation:

`P(A\cap B)=P(A|B)\cdot P(B)`

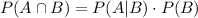
And substitute the known values:

`P(A\cap B)=(5)/(6)\cdot(3)/(5)`

We multiply the fractions and get the following result:

`\begin{gathered} P(A\cap B)=(5\cdot3)/(6\cdot5) \\ P(A\cap B)=(15)/(30) \end{gathered}`

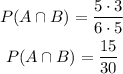
Finally, we simplify the fraction by dividing both numbers in the fraction by 15:

`P(A\cap B)=(1)/(2)`

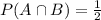
Answer: 1/2