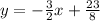Question

The line with slope m=-3/2 and passing through the midpoint of the line segment connecting (3,-2) and (-1/2,4). Leave in Standard Form.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about equation of lines and midpoints.

First, given a point (x0, y0), the equation of the line with slope m that passes through this point can be found by the point-slope formula:

`y-y_0=m\cdot(x-x_0)`

The standard form of a line equation is:

`y=mx+b`

Which is the same as the first, when defining:

`b=y_0-m\cdot x_0`

In this case, we need to find the midpoint of a segment in order to find a point of the line we want to determine the equation.

Remember that given two points (x1, y1) and (x2, y2), the midpoint (xM, yM) can be found by taking the mean of the x and y values of the points:

`\begin{gathered} x_M=(x_1+x_2)/(2) \\ y_M=(y_1+y_2)/(2) \end{gathered}`

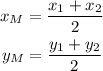
Knowing the points (3, -2) and (-1/2, 4), the midpoint of the segment connecting these points have coordinates:

`\begin{gathered} x_M=(3-(1)/(2))/(2)=(5)/(4) \\ y_M=(-2+4)/(2)=1 \end{gathered}`

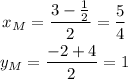
So the point of the line we want to find the equation if (5/4, 1) and its slope was given: m = -3/2.

We calculate b:

`b=1-\mleft(-(3)/(2)\mright)\cdot(5)/(4)=1+(15)/(8)=(23)/(8)`

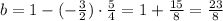
And the equation of the line is finally:

`y=-(3)/(2)x+(23)/(8)`