Question

. Given A(2,5), B(6, -11), C(3, 10), and D(2, 14) determine the relationship between AB and CD?

Answer 1

hello

we need to find if AB and CD are parallel or perpendiular. to do this, we compare slopes

now we should find slope of AB

`\begin{gathered} \text{slope of AB=}(y_2-y_1)/(x_2-x_1) \\ y_2=-11 \\ y_1=5 \\ x_2=6 \\ x_1=2 \\ AB=(-11-5)/(6-2) \\ AB=(-16)/(4) \\ AB=-4 \end{gathered}`

slope of CD

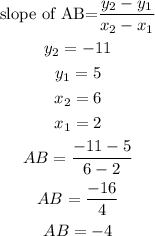
`\begin{gathered} CD=(y_2-y_1)/(x_2-x_1) \\ y_2=14 \\ y_1=10 \\ x_2=2 \\ x_1=3 \\ CD=(14-10)/(2-3) \\ CD=(4)/(-1) \\ CD=-4 \end{gathered}`

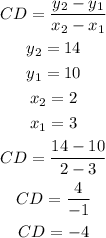
since both slopes are equal, then the lines must be parallel to each other.

you can also use a graph to solve this