Question

Find the x and y intercepts for the graph 2x+3y =0. And explain why two additional points should be found for the graph, and graph the function.

Answer 1

The x-intercept of a graph is the value of x for the points where the graph crosses the x axis, which happens when y=0.

The y-intercept of a graph is the value of y for the point where the graph crosses the y-axis, which happens when x=0.

Set x=0 to find the y-intercept of the graph:

`\begin{gathered} y=0 \\ 2x+3y=0\Rightarrow2x+3(0)=0 \\ \Rightarrow2x=0 \\ \Rightarrow x=0 \end{gathered}`

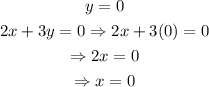
Set y=0 to find the x-intercept of the graph:

`\begin{gathered} x=0 \\ 2x+3y=0\Rightarrow2(0)+3y=0 \\ \Rightarrow3y=0 \\ \Rightarrow y=0 \end{gathered}`

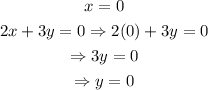
Notice that we got the same point, (0,0), for both the y-intercept and the x-intercept. This happens because this line passes through the origin of the coordinate system.

An additional value for the pair (x,y) would be needed in order to graph the function, since we can draw a straight line between any pair of points, but we just have one point.

Therefore, the x and y intercepts are:

x-intercept: 0

y-intercept: 0

Substitute another value of x or y into the equation 2x+3y=0 to find another point. For instance, use y=2 and solve for x:

`\begin{gathered} 2x+3(2)=0 \\ \Rightarrow2x+6=0 \\ \Rightarrow2x=-6 \\ \Rightarrow x=-(6)/(2) \\ \Rightarrow x=-3 \end{gathered}`

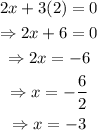
Then, the point (-3,2) also belongs to the graph.

Plot the points (-3,2) and (0,0). Then, draw a straight line through them to graph the function: