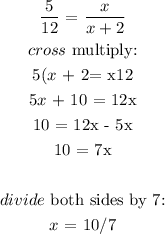Question

Pls explain this goof I have a final for it number 4

Answer 1

Answer:
`\begin{gathered} The\text{ proportion:} \\ (5)/(12)\text{ = }(x)/(x+2) \end{gathered}`

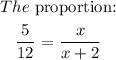
The value of x is 10/7

Step-by-step explanation:

Given:

4) Triangle ABC is similar to triangle DEF

side AB = 5, side BC = x

side EF = x + 2. side DE = 12

To find:

to draw the triangles, write the proportion and solve for x

First, we need to draw the triangles using the given information:

In similar triangles, the ratios of the corresponding sides are equal

For Triangle ABC similar to triangle DEF

AB corresponds to DE

BC corresponds to EF

AC corresponds to DF

The ratio of the corresponding sides will give the proportion:

`\begin{gathered} (AB)/(DE)\text{ = }(BC)/(EF)\text{ = }(AC)/(DF) \\ \\ Since\text{ we don't have values for AC abd DF, we will use the first two ratios:} \\ (AB)/(DE)\text{ = }(BC)/(EF)\text{ } \end{gathered}`
`\begin{gathered} The\text{ proportion:} \\ (5)/(12)\text{ = }(x)/(x+2) \end{gathered}`

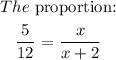
Finally, we will solve for x:

`\begin{gathered} (5)/(12)\text{ = }(x)/(x+2) \\ cross\text{ multiply:} \\ 5(x\text{ + 2\rparen = x\lparen12\rparen} \\ 5x\text{ + 10 = 12x} \\ 10\text{ = 12x - 5x} \\ 10\text{ = 7x} \\ \\ divide\text{ both sides by 7:} \\ x\text{ = 10/7} \end{gathered}`