Question

21 + 23 + 25 + ⋯ + 43Find the sum of the arithmetic series

Answer 1

we want to find the sum of the aritmetic series 21 + 23 + 25 + ⋯ + 43

From the series, we have

`\begin{gathered} a=first\text{ term = 21} \\ d=common\text{ difference = 2} \\ Tn=last\text{ term = 43} \\ n=number\text{ of terms = }? \end{gathered}`

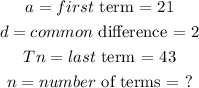
we don't know the number of terms, so let's find it using the formula

`\begin{gathered} Tn=a+(n-1)d \\ 43=21+(n-1)2 \\ 43=21+2n-2 \\ 43=19+2n \\ 2n=43-19 \\ 2n=24 \\ n=(24)/(2) \\ n=12\text{ terms } \end{gathered}`

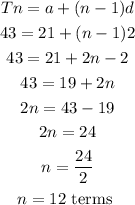
So we have the number of terms as 12.

To find the sum, we use the formula

`\begin{gathered} S=(n)/(2)[2a+(n-1)d] \\ where\text{ S = sum} \end{gathered}`

Applying, we have

`\begin{gathered} S=(12)/(2)[2*21+(12-1)2] \\ S=6[42+(11)2] \\ S=6[42+22] \\ S=6[64] \\ S=6*64 \\ S=384 \end{gathered}`

Hence the answer is 384