Question

A card is drawn from a well-shuffled deck of 52 cards. What is the probability of drawing an ace or a 6?A. 13/2B. 7/26C. 6/52D. 2/13

Answer 1

Step 1

State the expression for the probability of an event to occur.

`\text{The probability of an event =}\frac{number\text{ of required events}}{\text{Total number of events}}`

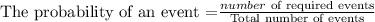
Step 2

Find out the number of required events

Total number of events = 52 cards

`\begin{gathered} A\text{ deck of cards has} \\ 4\text{ Suites - }hearts,\text{ clubs, spade and diamond.} \\ \text{and each suite has} \\ \mleft\lbrace ace,\text{ 2,3,4,5,6,7,8,9, jack, qu}een,\text{ king}\mright\rbrace \end{gathered}`

Therefore, the number of aces = 4

The number of 6 = 4

Step 3

Find the probability of getting an ace or a 6.

`\begin{gathered} \text{The probability of getting an ace =}\frac{number\text{ of aces in a deck of cards}}{\text{Total number of cards}} \\ \text{The probability of getting an ace}=(4)/(52) \\ \text{The probability of g}etting\text{ a 6 =}\frac{number\text{ of 6 in a deck of cards}}{\text{Total number of cards}} \\ \text{The probability of g}etting\text{ a 6}=(4)/(52) \end{gathered}`

Therefore,

`\text{The probability of drawing an ace or a 6 = }(4)/(52)+(4)/(52)=(8)/(52)=(2)/(13)`

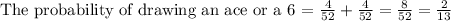
Hence, Option D