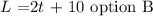Question

A lighting designer created a program for the opening of a stage show when the show starts 10 lights are on every 30 seconds One more light comes on if t is time in minutes and L is the number of lights that are on which function best models the number of lights that are on after T minutes of the Stacia

Answer 1

Answer:
`L\text{ =2}t\text{ + 10 \lparen option B\rparen}`

Step-by-step explanation:

Given:

number lights on when the show starts = 10

the rate at which the light comes on = 30 seconds per light

t = time in minutes

L = number of lights on

To find:

the function that bests models the number of lights after t minutes

To determine the function, we will apply linear function formula:

`\begin{gathered} y\text{ = mx + b} \\ b\text{ = initial amount} \\ m\text{ = rate } \\ x\text{ = t } \\ y\text{ = L} \end{gathered}`

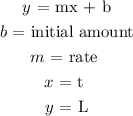
The initial number of lights = 10

b = 10

since t is in minutes, we need to convert the rate from seconds to minutes

30 seconds = 1 light

60 seconds = 2(30 seconds)

60 seconds = 2(1) = 2 lights

rate = m = 2 lights/min

substitute the values:

`L\text{ =2}t\text{ + 10 \lparen option B\rparen}`