SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given sides
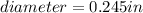
STEP 2: Write the given formula for cross sectional area
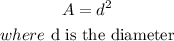
STEP 3: Find the cross sectional area
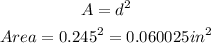
STEP 4: Convert to circular mils
A circular mil is the equivalent area of a circle whose diameter is 0.001 (10-3) inch, or approximately 0.7854 millionths of a square inch.

Hence, the cross sectional area of the wire is 60025 circular mils