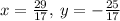Given
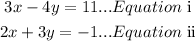
Using Elimination method
Solution
Multiply the first equation by 3 and multiply the second equation by 4.
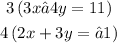
Becomes
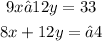
Add these equations to eliminate y:
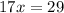
Divide both sides by 17
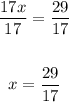
Now that we've found x let's plug it back in to solve for y.
Write down an original equation:
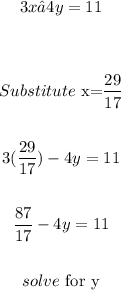
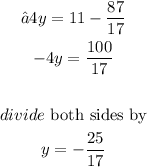
The final answer