Question

The length of a rectangle is five times its width. If the perimeter of the rectangle is 120 ft, find its area.

Answer 1

The length of a rectangle is five times its width.

Let the length be represented by L

Let the width be represented by W

The length of the rectangle is five times the width i.e

`L=5W`

To find the perimeter, P, of a rectangle, the formula is

`P=2(L+W)`

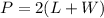
Given that the perimeter, P, of the rectangle is 120ft,

Subsitute for length and width into the formula above

`\begin{gathered} P=2(L+W) \\ 120=2(5W+W) \\ 120=2(6W) \\ 120=12W \\ \text{Divide both sides by 12} \\ (12W)/(12)=(120)/(12) \\ W=10ft \end{gathered}`

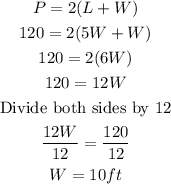
Recall that, the length of the rectangle is

`\begin{gathered} L=5W \\ L=5(10) \\ L=50ft \\ W=10ft \end{gathered}`

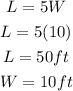
To find the area, A, of a rectangle, the formula is

`A=LW`

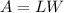
Substitute the values of the length amd width into the formula above

`\begin{gathered} A=(50)(10)=500ft^2 \\ A=500ft^2 \end{gathered}`

Hence, the area of the rectangle is 500ft²