Question

Geometry_I dont know how to calculate 80/360 pie r^2

Answer 1

Hello there. To solve this question, we'll have to remember some properties about circular sectors.

Given a circular sector of a circle with radius R:

Suppose the length of the arc AB is alpha (in radians).

From a well-known theorem about angles in a circle, we know that the angle generating this arc from the center has the same measure, that is:

So we want to determine the area of the sector knowing the radius and the length of the arc.

First, we know that the area of the full circle is given by:

`A=\pi\cdot R^2`

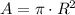
The sector is a fraction of this circle, that means that:

`A=kA_(sector)`

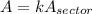
A is a multiple of Asector.

In fact, this proportionality constant is the ratio between the central angle and the angle alpha forming the sector, that is

`k=(2\pi)/(\alpha)`

It is also possible to have alpha in degrees, but we have to convert the center angle to degrees as well, so we get

`k=(2\pi\cdot(180^(\circ))/(\pi))/(\alpha\cdot(180^(\circ))/(\pi))=(360^(\circ))/(\alpha^(\circ))`

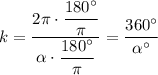
As we want to solve for the area of the sector, we have that:

`A_(sector)=A\cdot\frac{\alpha^(\circ)}{{360^(\circ)}}=(\alpha^(\circ))/(360^(\circ))\cdot\pi R^2`

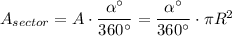
Okay. With this, we can solve the question.

We have the following circle:

In this case, notice R = 18 yd and the length of the arc is 80º. This gives us the angle alpha:

Now, we take the ratio between the angle and the total angle applying the formula:

`A_(sector)=(80^(\circ))/(360^(\circ))\cdot\pi\cdot18^2`

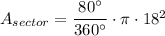
Square the number

`A_(sector)=(80^(\circ))/(360^(\circ))\cdot\pi\cdot324`

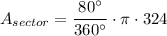
Simplify the fraction by a factor of 40º

`A_(sector)=(2)/(9)\cdot\pi\cdot324`

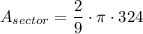
Multiply the numbers and simplify the fraction

`A_(sector)=(648\pi)/(9)=72\pi`

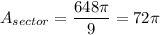
This is the area of this sector.