Given
The equation,

To find all the solutions of the given equation in polar form.
Step-by-step explanation:
It is given that,

That implies,
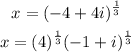
Now, consider
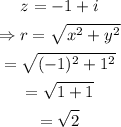
Also,
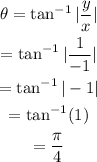
Since (x,y) lies in 2nd quadrant.
Then,
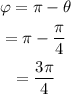
Therefore,

That implies,
![\begin{gathered} x=(4)^{(1)/(3)}\lbrace(√(2)e^^{i((3\pi)/(4))})\rbrace^{(1)/(3)} \\ =(2^2)^{(1)/(3)}(2^{(1)/(2)})^{(1)/(3)}(e^{i((3\pi)/(4))})^{(1)/(3)} \\ =\sqrt[6]{32}(e^{i((3\pi)/(4))})^{(1)/(3)} \\ =\sqrt[6]{32}\lbrace cis((3\pi)/(4))\rbrace^{(1)/(3)} \end{gathered}]()
Now,
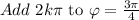
That implies,
![x=\sqrt[6]{32}\lbrace cis((3\pi)/(4)+2k\pi)\rbrace^{(1)/(3)}](https://img.qammunity.org/2023/formulas/mathematics/college/lllyt58z4mdxcrgh0k8m5cizjs0s31zivm.png)
By applying De-movers theorem,
![x=\sqrt[6]{32}\lbrace cis(1)/(3)((3\pi)/(4)+2k\pi)\rbrace](https://img.qammunity.org/2023/formulas/mathematics/college/mtahbj26hqyca0jhd8p0h3y6cvqrv961h7.png)
Put k=0,1,2 in the above equation.
That implies,
![\begin{gathered} When\text{ }k=0, \\ x=\sqrt[6]{32}\lbrace cis(1)/(3)((3\pi)/(4))\rbrace \\ =\sqrt[6]{32}\lbrace cis((\pi)/(4))\rbrace \\ When\text{ }k=1, \\ x=\sqrt[6]{32}\lbrace cis(1)/(3)((3\pi)/(4)+2\pi)\rbrace \\ =\sqrt[6]{32}\lbrace cis(1)/(3)((3\pi+8\pi)/(4))\rbrace \\ =\sqrt[6]{32}\lbrace cis((11\pi)/(12))\rbrace \\ When\text{ }k=2, \\ x=\sqrt[6]{32}\lbrace cis(1)/(3)((3\pi)/(4)+4\pi)\rbrace \\ =\sqrt[6]{32}\lbrace cis(1)/(3)((3\pi+16\pi)/(4))\rbrace \\ =\sqrt[6]{32}\lbrace cis((19\pi)/(12))\rbrace \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/51g9mc708dwxudkf2qbius8nom3ii6jp3b.png)
Hence, the solutions are,
![x=\sqrt[6]{32}\lbrace cis((\pi)/(4))\rbrace,\sqrt[6]{32}\lbrace cis((11\pi)/(12))\rbrace,\sqrt[6]{32}\lbrace cis((19\pi)/(12))\rbrace](https://img.qammunity.org/2023/formulas/mathematics/college/n3dzl8aflp4pphjqhabba6jf2a85nmqb8h.png)