Question

6) Find the speed a spherical raindrop would attain by falling from 4.00 km. Do this:a) In the absence of air dragb) In the presence of air dragc) Assume that the diameter of the drop is 3 mm and the density of the water is 0.98x10^3 kg/m^3

Answer 1

We are asked to determine the velocity of a rain drop if it falls from 4 km.

To do that we will use the following formula:

`2ah=v_f^2-v_0^2`

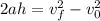
Where:

`\begin{gathered} a=\text{ acceleration} \\ h=\text{ height} \\ v_f,v_0=\text{ final and initial velocity} \end{gathered}`

If we assume the initial velocity to be 0 we get:

`2ah=v_f^2`

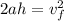
The acceleration is the acceleration due to gravity:

`2gh=v_f^2`

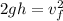
Now, we take the square root to both sides:

`√(2gh)=v_f`

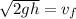
Now, we substitute the values:

`\sqrt{2(9.8(m)/(s^2))(4000m)}=v_f`

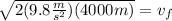
solving the operations:

`280(m)/(s)=v`

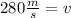
Therefore, the velocity without air drag is 280 m/s.

Part B. we are asked to determine the velocity if there is air drag. To do that we will use the following formula:

`F_d=(1)/(2)C\rho_(air)Av^2`

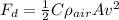
Where:

`\begin{gathered} F_d=drag\text{ force} \\ C=\text{ constant} \\ \rho_(air)=\text{ density of air} \\ A=\text{ area} \\ v=\text{ velocity} \end{gathered}`

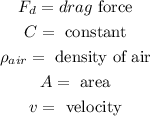
We need to determine the drag force. To do that we will use the following free-body diagram:

Since the velocity that the raindrop reaches is the terminal velocity and its a constant velocity this means that the acceleration is zero and therefore the forces are balanced:

`F_d=mg`

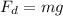
Now, we determine the mass of the raindrop using the following formula:

`m=\rho_(water)V`

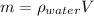
Where:

`\begin{gathered} \rho_(water)=\text{ density of water} \\ V=\text{ volume} \end{gathered}`

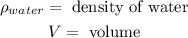
The volume is the volume of a sphere, therefore:

`m=\rho_(water)((4)/(3)\pi r^3)`

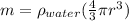
Since the diameter of the raindrop is 3 millimeters, the radius is 1.5 mm or 0.0015 meters. Substituting we get:

`m=(0.98*10^3(kg)/(m^3))((4)/(3)\pi(0.0015m)^3)`

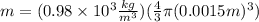
Solving the operations:

`m=1.39*10^(-5)kg`

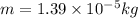
Now, we substitute the values in the formula for the drag force:

`F_d=(1.39*10^(-5)kg)(9.8(m)/(s^2))`

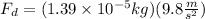
Solving the operations:

`F_d=1.36*10^(-4)N`

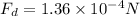
Now, we substitute in the formula:

`1.36*10^(-4)N=(1)/(2)C\rho_(air)Av^2`

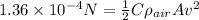
Now, we solve for the velocity:

`(1.36*10^(-4)N)/((1)/(2)C\rho_(air)A)=v^2`

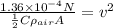
Now, we substitute the values. We will use the area of a circle:

`(1.36*10^(-4)N)/((1)/(2)(0.45)(1.21(kg)/(m^3))(\pi r^2))=v^2`

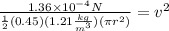
Substituting the radius:

`(1.36\cdot10^(-4)N)/((1)/(2)(0.45)(1.21(kg)/(m^(3)))(\pi(0.0015m)^2))=v^2`

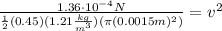
Solving the operations:

`70.67(m^2)/(s^2)=v^2`

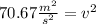
Now, we take the square root to both sides:

`\begin{gathered} \sqrt{70.67(m^2)/(s^2)}=v \\ \\ 8.4(m)/(s)=v \\ \end{gathered}`

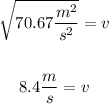
Therefore, the velocity is 8.4 m/s