ANSWER:
A = 48.19°
B = 48.19°
C = 83.62°
Explanation:
Given:
a = 6, b = 6, c = 8
We can calculate the angles by means of the law of cosines, just like this:
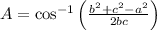
We apply in each case to calculate the 3 angles, as follows:
![\begin{gathered} A=\cos^(-1)\left((6^2+8^2-6^2)/(2\left(6\right)\left(8\right))\right)=\cos^(-1)\left((2)/(3)\right) \\ \\ A=48.19^(\circ\:) \\ \\ B=\cos^(-1)\left((6^2+8^2-6^2)/(2\left(6\right)\left(8\right))\right)=\cos^(-1)\left((2)/(3)\right) \\ \\ B=48.19^{\operatorname{\circ}} \\ \\ C=\cos^(-1)\left((6^2+6^2-8^2)/(2\left(6\right)\left(6\right))\right)=\cos^(-1)\left((1)/(9)\right) \\ \\ C=83.62^(\circ\:) \end{gathered}]()
Therefore, the angles are the following:
A = 48.19°
B = 48.19°
C = 83.62°