Question

For each ordered pair, determine whether it is a solution to the system of equations:7x - 4y = 8-2x+3y=7

Answer 1

The solution to the system of equations is

(x, y) = (4, 5)

Step-by-step explanation:

Given the pair of equations:

`\begin{gathered} 7x-4y=8\ldots.\ldots..\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\text{.}\mathrm{}(1) \\ -2x+3y=7\ldots\ldots\ldots\ldots\ldots.\ldots\ldots\ldots\ldots\ldots\ldots\ldots\text{.}\mathrm{}(2) \end{gathered}`

To know the solution to the system, we solve the equations simultaneously.

From equation (1), making x the subject, we have:

`x=(8+4y)/(7)\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\text{.}(3)`

Substituting equation (3) in (2)

`\begin{gathered} -2((8+4y)/(7))+3y=7 \\ \\ \text{Multiply both sides by 7} \\ \\ -2(8+4y)+21y=49 \\ -16-8y+21y=49 \\ -16+13y=49 \\ \\ \text{Add 16 to both sides} \\ -16+13y+16=49+16 \\ 13y=65 \\ \\ \text{Divide both sides by 13} \\ y=(65)/(13)=5 \end{gathered}`

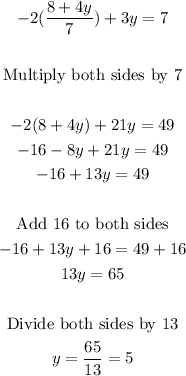
The value of y is 5

Using y = 5 in equation (3)

`\begin{gathered} x=(8+4(5))/(7) \\ \\ =(8+20)/(7) \\ \\ =(28)/(7) \\ \\ =4 \end{gathered}`

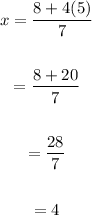
The value of x is 4