Question

The cholesterol levels of an adult can be described by a normal model with a mean of 185 mg/dL and a standard deviation of 29. What percent of adults do you expect to have cholesterol levels over 190 mg/dL?

Answer 1

Given

mean = 185 mg/dL

standard deviation = 29

Required: The percent of adults that have cholesterol levels over 190 mg/dL

Step 1: Find the z-score for the given cholesterol level using the formula:

`\begin{gathered} z\text{ = }\frac{x\text{ - }\mu}{\sigma} \\ Where\text{ }\mu\text{ is the mean} \\ and\text{ }\sigma\text{ is the standard deviation} \end{gathered}`

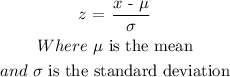
Substituting the given values:

`\begin{gathered} z\text{ = }\frac{190-\text{ 185}}{29} \\ z\text{ = 0.1724} \end{gathered}`

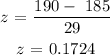
Step 2: Using a normal distribution table, find the probability of a random value greater than 0.1724

`P(x\text{ >}0.1724)\text{ = 0.43156}`

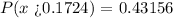
Step 3: Convert to percent by multiplying by 100%

`\begin{gathered} =\text{ 0.43156 }*\text{ 100} \\ =\text{ 43.156}\% \\ \approx\text{ 43.2\%} \end{gathered}`

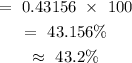
Hence, the percent of adults that should have a cholesterol level greater than 190 mg/dL is 43,2%