We need the time t in the compound interest formula:

Then, if we move P to the left hand side, we get
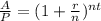
If we apply logarithm in both sides, we obtain
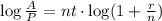
therefore, the time is given by
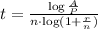
In our case A= $33467.27 (Amount), P=$32000 (Principal), n=0.03 (interest rate) and n=4 (quarterly interest).
By substituting these values into the last formula, we have
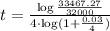
which gives
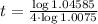
the, the time is
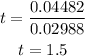
that is, the time will be equal to 1.5 years.