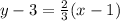The line:

can be written as:
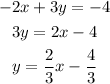
from this form we notice that its slope is 2/3.
We know that two lines are parallel if and only if their slopes are equal, this measn the lie we are looking for has slope 2/3 also.
Once we know the slope of the second line and since we know a point of it we can use the equation of a line:

Plugging the values we have that the equation we are looking for is: