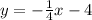Question

Determine the equation of the line with y intercept at (0,-4) and a slip of - 1/4.

Answer 1

We need to determine the equation of the line that passes through (0, -4) and has a slope of -1/4. For that we will first use the slope-point form, and then isolate the y-variable on the left side to determine the slope-intercept form. The two forms are shown below:

`\begin{gathered} y-y_1=m\cdot(x-x_1) \\ y=m\cdot x+b \end{gathered}`

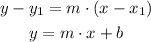
Since we have the value of the slope, and a point we can determine the first equation.

`\begin{gathered} y-(-4)=-(1)/(4)\cdot(x-0) \\ y+4=-(1)/(4)x \\ \end{gathered}`

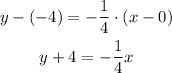
Now we need to isolate the y-variable on the left side.

`y=-(1)/(4)x-4`