Given:
There are given the expression:
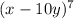
Step-by-step explanation:
According to the question:
We need to find the 4th term in the expansion.
So,
From the given expression:
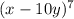
To find the 4th expansion, we will use the binomial theorem:
So,
From the binomial expansion:
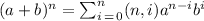
Then,
Use the above formula in the given expression:
So,
From the given expression:

Then,
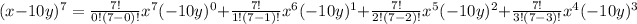
Then,
![\begin{gathered} (x-10y)^(7)=(7!)/(0!(7-0)!)x^(7)(-10y)^(0)+(7!)/(1!(7-1)!)x^(6)(-10y)^(1)+(7!)/(2!(7-2)!)x^(5)(-10y)^(2)+(7!)/(3!(7-3)!)x^(4)(-10y)^(3) \\ (x-10y)^7=x^7-70x^6y+2100x^5y^2-35000x^4y^3 \end{gathered}]()
So,
The 4th term of the given expansion is shown below:
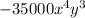
Final answer:
Hence, the correct option is B.