Question

At the Royal Dragon Chinese restaurant, a slip in the fortune cookies indicates a dollar amount that will be subtracted from your total bill. A bag of 10 fortune cookies is given to you from which you will select one. If five fortune cookies contain "$1off." four contain "$2 off." and one contains "$5 off." determine the expectation of a selection.

Answer 1

$1.8

Step-by-step explanation:

Given:

A bag of 10 fortune cookies;

Five fortune cookies contain "$1 off"

Four contain "$2 off"

One contains "$5 off"

So the probability of selecting a "$1 off" cookie will be;

`\begin{gathered} P(\text{\$1 }off\text{ }cookie)=(5)/(10) \\ =(1)/(2) \end{gathered}`

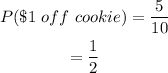
And the probability of selecting a "$2 off" cookie will be;

`\begin{gathered} P(\text{\$2 }off\text{ }cookie)=(4)/(10) \\ =(2)/(5) \end{gathered}`

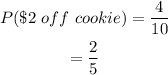
the probability of selecting a "$5 off" cookie will be;

`\begin{gathered} P(\text{\$5 }off\text{ }cookie)=(1)/(10) \\ \end{gathered}`

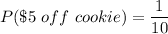
We can determine the expectation of a selection as seen below;

`\begin{gathered} Expectation=(1*(1)/(2))+(2*(2)/(5))+(5*(1)/(10)) \\ \\ =(1)/(2)+(4)/(5)+(1)/(2) \\ \\ =(9)/(5) \\ \\ =\text{ \$}1.8\text{ }off \end{gathered}`

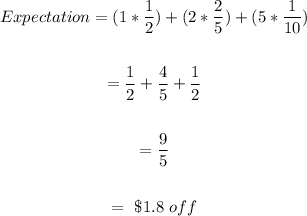
So the expectation of a selection will be $1.8 off