Solution:
Given a right triangle;
Where the long leg, x, is, the side opposite the angle 60°
And the short leg, y, is the side opposite angle 30°
To find the ratio of the long leg to short leg,

For the short leg
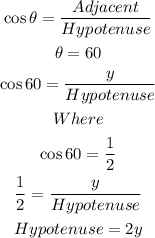
The ratio of the long and short leg will be
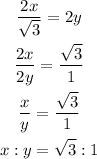
Hence, the answer is B.