Question

Question 13 of 28Which of the following represents the ratio of the long leg to the short leg inthe right triangle shown below?30O A. 1:4√3OB. √3:1O C. 1:2O D. 2:160°

Answer 1

Given a right triangle;

Where the long leg, x, is, the side opposite the angle 60°

And the short leg, y, is the side opposite angle 30°

To find the ratio of the long leg to short leg,

`\begin{gathered} For\text{ long leg} \\ \sin\theta=(Opposite)/(Hypotenuse) \\ Where \\ \theta=60\degree \\ \sin60\degree=(x)/(Hypotenuse) \\ (√(3))/(2)=(x)/(Hypotenuse) \\ Hypotenuse=(2x)/(√(3)) \end{gathered}`

For the short leg

`\begin{gathered} \cos\theta=(Adjacent)/(Hypotenuse) \\ \theta=60\degree \\ \cos60\degree=(y)/(Hypotenuse) \\ Where \\ \cos60\degree=(1)/(2) \\ (1)/(2)=(y)/(Hypotenuse) \\ Hypotenuse=2y \end{gathered}`

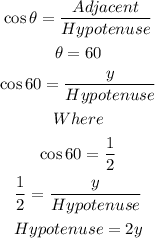
The ratio of the long and short leg will be

`\begin{gathered} (2x)/(√(3))=2y \\ (2x)/(2y)=(√(3))/(1) \\ (x)/(y)=(√(3))/(1) \\ x:y=√(3):1 \end{gathered}`

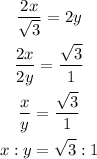
Hence, the answer is B.