Question

Consider the line 2x +5y = -2.(a) What is the slope of a line parallel to this line?(b) What is the slope of a line perpendicular to this line?

Answer 1

(a) Parallel slope = -2/5

(b) Perpendicular slope = 5/2

Explanation:

We have the following equation:

`2x+5y=-2`

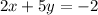
To determine the slope, we solve for y, like so:

`\begin{gathered} 5y=-2-2x \\ y=-(2)/(5)-(2)/(5)x \end{gathered}`

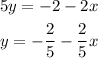
The slope is the quotient of x, so the slope of the line is -2/5

(a)

When two lines are parallel the slope is the same.

Therefore :

m = -2/5

(b)

Now, when the lines are perpendicular, the product of both slopes is equal to -1, just like this:

`\begin{gathered} m_1\cdot m_2=-1 \\ -(2)/(5)\cdot m_2=-1 \\ m_2=(5)/(2) \end{gathered}`

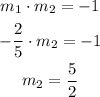
(a) Parallel slope = -2/5

(b) Perpendicular slope = 5/2