Question

WXYZ is translated 6 units to the left and then reflected in the x-axis to create W'X'Y'Z'. Write an ordered pair to show the location of each vertex of the transformed figure.

Answer 1

Step 1: Write out the coordinates of W,X,Y, and Z

`\begin{gathered} \text{ The coordinates of W }=(5,9) \\ \text{ The coordinates of X }=(7,8) \\ \text{ The coordinates of Y }=(9,2) \\ \text{ The coordinates of Z }=(2,5) \end{gathered}`

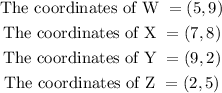
Step2: Write out the rule to translate a point (x,y) by k units to the left, where k is a positive number

`(x,y)\to(x-k,y)`

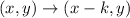
Step 3: Translate the coordinates of W,X,Y, and Z to the left by 6 units

`\begin{gathered} \text{The coordinates of W translated 6 units to the left }=(5-6,9)=M(-1,9) \\ \text{The coordinates of X translated 6 units to the left }=(7-6,8)=N(1,8) \\ \text{The coordinates of Y translated 6 units to the left }=(9-6,2)=O(3,2) \\ \text{The coordinates of Z translated 6 units to the left }=(2-6,5)=P(-4,5) \end{gathered}`

Step4: Write out the rule to reflect a point (a,b) over the x-axis

`(a,b)\to(a,-b)`

Step 5: Reflect the coordinates of M,N,O, and P over the x-axis to get the coordinates of W', X', Y', and Z' respectively

`\begin{gathered} \text{The coordinates of M reflected over the x-axis }=W^(\prime)(-1,-9) \\ \text{The coordinates of N reflected over the x-axis }=X^(\prime)(1,-8) \\ \text{The coordinates of O reflected over the x-axis }=Y^(\prime)(3,-2) \\ \text{The coordinates of P reflected over the x-axis }=Z\prime^{}(-4,-5) \end{gathered}`

Step 6: Write an ordered pair to show the location of each vertex of the transformed figure

The location of W' = (-1, -9)

The location of X' = (1, -8)

The location of Y' = (3, -2)

The location of Z' = (-4, -5)