The domain of a function is given by all the set of x values for which the function is defined. In this case we have the function:
![f(x)=\sqrt[]{19-x}](https://img.qammunity.org/2023/formulas/mathematics/college/iwrrj8pa06wn7h1wisid64ptkczuqoee88.png)
There's a key factor here that we must note. When we are working with real functions like this one the square root of negative numbers is not defined. This means that for any function with a square root and a variable x inside we have that the x values that makes the term inside the root negative are not part of the domain. Taking this into account is easy to see that the domain of f(x) is given by all those x values that make the term 19-x equal or greater than 0. Then we have:
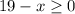
We can add x to both sides of this inequality:

So this means that if x is equal or smaller than 19 then the function is defined. Then the domain of the function written in set notation is:
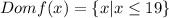
And that's the answer to this question.